If a constant force F is applied to a particle that achieves a displacement Δr, the work done by the force is defined as the scalar product of the force and displacement vectors:
More generally, if the force varies as a function of position as the particle moves from r1 to r2 along a path C, the work done on the particle is given by the line integral
If the work done in moving the particle from r1 to r2 is the same no matter what path is taken, the force is said to be conservative. Gravity is a conservative force, as is the force due to an idealized spring, as given by Hooke's law. The force due to friction is non-conservative.
The kinetic energy Ek of a particle of mass m travelling at speed v is given by
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
The work-energy theorem states that for a particle of constant mass m the total work W done on the particle from position r1 to r2 is equal to the change in kinetic energy Ek of the particle:
Conservative forces can be expressed as the gradient of a scalar function, known as the potential energy and denoted Ep:
If all the forces acting on a particle are conservative, and Ep is the total potential energy (which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
This result is known as conservation of energy and states that the total energy,
is constant in time. It is often useful, because many commonly encountered forces are conservative.


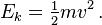


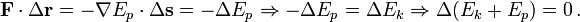

No comments:
Post a Comment