CLASSICAL MECHANICS: List of equations in classical mechanics

Nomenclature

a = acceleration (m/s²)

g = gravitational field strength/acceleration in free-fall (m/s²)

F = force (N = kg m/s²)

E_k = kinetic energy (J = kg m²/s²)

E_p = potential energy (J = kg m²/s²)

m = mass (kg)

p = momentum (kg m/s)

s = displacement (m)

R = radius (m)

t = time (s)

v = velocity (m/s)

v₀ = velocity at time t=0

W = work (J = kg m²/s²)

τ = torque (m N, not J) (torque is the rotational form of force)

s(t) = position at time t

s₀ = position at time t=0

r_unit = unit vector pointing from the origin in polar coordinates

θ_unit = unit vector pointing in the direction of increasing values of theta in polar coordinates

Note: All quantities in bold represent vectors.]

Center of mass

Discrete case:

$\mathbf{s}_{\hbox{CM}} = {1 \over m_{\hbox{total}}} \sum_{i = 1}^{n} m_i \mathbf{s}_i$
where n is the number of mass particles.
Continuous case:
$\mathbf{s}_{\hbox{CM}} = {1 \over m_{\hbox{total}}} \int \rho(\mathbf{s}) dV$
where ρ(s) is the scalar mass density as a function of the position vector

Velocity
$\mathbf{v}_{\mbox{average}} = {\Delta \mathbf{d} \over \Delta t}$
$\mathbf{v} = {d\mathbf{s} \over dt}$

Acceleration
$\mathbf{a}_{\mbox{average}} = \frac{\Delta\mathbf{v}}{\Delta t}$
$\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d^2\mathbf{s}}{dt^2}$
Centripetal Acceleration

$|\mathbf{a}_c | = \omega^2 R = v^2 / R$
(R = radius of the circle, ω = v/R angular velocity)
Momentum
$\mathbf{p} = m\mathbf{v}$

Force
$\sum \mathbf{F} = \frac{d\mathbf{p}}{dt} = \frac{d(m\mathbf{v})}{dt}$
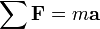$\sum \mathbf{F} = m\mathbf{a} \quad\$    (Constant Mass)

Impulse
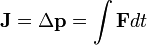
$\mathbf{J} = \Delta \mathbf{p} = \int \mathbf{F} dt$
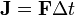$\mathbf{J} = \mathbf{F} \Delta t \quad\$
   if F is constant

Moment of inertia
For a single axis of rotation: The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
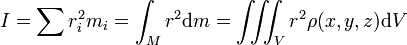
$I = \sum r_i^2 m_i =\int_M r^2 \mathrm{d} m = \iiint_V r^2 \rho(x,y,z) \mathrm{d} V$

Angular momentum
$|L| = mvr \quad\$
   if v is perpendicular to r
Vector form:
$\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{I}\, \omega$
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor of rank-2)
r is the radius vector.

Torque
$\sum \boldsymbol{\tau} = \frac{d\mathbf{L}}{dt}$
$\sum \boldsymbol{\tau} = \mathbf{r} \times \mathbf{F} \quad$
if |r| and the sine of the angle between r and p remains constant.
$\sum \boldsymbol{\tau} = \mathbf{I} \boldsymbol{\alpha}$
This one is very limited, more added later. α = dω/dt

Precession
Omega is called the precession angular speed, and is defined:
$\boldsymbol{\Omega} = \frac{wr}{I\boldsymbol{\omega}}$
(Note: w is the weight of the spinning flywheel)
Energy
for m as a constant:
$\Delta E_k = \int \mathbf{F}_{\mbox{net}} \cdot d\mathbf{s} = \int \mathbf{v} \cdot d\mathbf{p} = \begin{matrix}\frac{1}{2}\end{matrix} mv^2 - \begin{matrix}\frac{1}{2}\end{matrix} m{v_0}^2 \quad\$
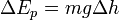$\Delta E_p = mg\Delta h \quad\ \,\!$ in field of gravity

Central force motion
$\frac{d^2}{d\theta^2}\left(\frac{1}{\mathbf{r}}\right) + \frac{1}{\mathbf{r}} = -\frac{\mu\mathbf{r}^2}{\mathbf{l}^2}\mathbf{F}(\mathbf{r})$

Equations of motion (constant acceleration)
These equations can be used only when acceleration is constant. If acceleration is not constant then calculus must be used.
$v = v_0+at \,$
$s = \frac {1} {2}(v_0+v) t$
$s = v_0 t + \frac {1} {2} a t^2$
$v^2 = v_0^2 + 2 a s \,$
These equations can be adapted for angular motion, where angular acceleration is constant:
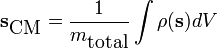
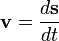
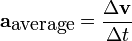
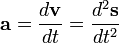
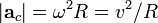
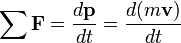
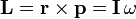
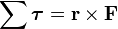
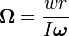
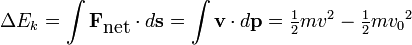
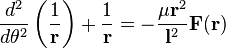
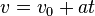
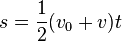
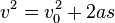
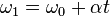
$\omega _1 = \omega _0 + \alpha t \,$
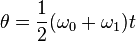
$\theta = \frac{1}{2}(\omega _0 + \omega _1)t$
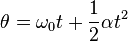
$\theta = \omega _0 t + \frac{1}{2} \alpha t^2$
$\omega _1^2 = \omega _0^2 + 2\alpha\theta$
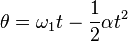
$\theta = \omega _1 t - \frac{1}{2} \alpha t^2$

CLASSICAL MECHANICS

Friday, June 25, 2010

List of equations in classical mechanics

Velocity

Acceleration

Momentum

Force

Impulse

Moment of inertia

Angular momentum

Torque

Precession

Energy

Central force motion

Equations of motion (constant acceleration)

No comments:

Post a Comment