Description of the theory
The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects which classical mechanics can describe always have a non-zerosize. (The physics of very small particles, such as the electron, is more accurately described byquantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseballcan spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.
Velocity and speed
The position of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle. In general, the point particle need not be stationary relative to O, so r is a function of t, the timeelapsed since an arbitrary initial time. In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumesEuclidean geometry for the structure of space.
The velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time or
In classical mechanics, velocities are directly additive and subtractive. For example, if one car traveling East at 60 km/h passes another car traveling East at 50 km/h, then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, from the perspective of the faster car, the slower car is moving 10 km/h to the West. Velocities are directly additive as vector quantities; they must be dealt with using vector analysis.
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector u = ud and the velocity of the second object by the vector v = ve, where u is the speed of the first object, v is the speed of the second object, and d and e are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is
Similarly,
When both objects are moving in the same direction, this equation can be simplified to
Or, by ignoring direction, the difference can be given in terms of speed only:
Acceleration
The acceleration, or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time) or
Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both. If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration, but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.
Frames of reference
While the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames. They are characterized by the absence of acceleration of the observer and the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth). A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame. A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are unaccelerated with respect to the distant stars are regarded as good approximations to inertial frames.
Consider two reference frames S and S' . For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x′,y′,z′,t′) in frame S′. Assuming time is measured the same in all reference frames, and if we require x = x' when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S′ and S, which are moving at a relative velocity of u in the x direction is:
- x′ = x − ut
- y′ = y
- z′ = z
- t′ = t
This set of formulas defines a group transformation known as the Galilean transformation (informally, the Galilean transform). This group is a limiting case of the Poincaré group used in special relativity. The limiting case applies when the velocity u is very small compared to c, thespeed of light.
The transformations have the following consequences:
- v′ = v − u (the velocity v′ of a particle from the perspective of S′ is slower by u than its velocity v from the perspective of S)
- a′ = a (the acceleration of a particle is the same in any inertial reference frame)
- F′ = F (the force on a particle is the same in any inertial reference frame)
- the speed of light is not a constant in classical mechanics, nor does the special position given to the speed of light in relativistic mechanics have a counterpart in classical mechanics.

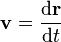 .
.



 .
.
No comments:
Post a Comment