This blog will help you to know about some of the basic things that a mechanical engineer must not fail to know
Saturday, June 26, 2010
Friday, June 25, 2010
List of equations in classical mechanics
- Nomenclature
- a = acceleration (m/s²)
- g = gravitational field strength/acceleration in free-fall (m/s²)
- F = force (N = kg m/s²)
- Ek = kinetic energy (J = kg m²/s²)
- Ep = potential energy (J = kg m²/s²)
- m = mass (kg)
- p = momentum (kg m/s)
- s = displacement (m)
- R = radius (m)
- t = time (s)
- v = velocity (m/s)
- v0 = velocity at time t=0
- W = work (J = kg m²/s²)
- τ = torque (m N, not J) (torque is the rotational form of force)
- s(t) = position at time t
- s0 = position at time t=0
- runit = unit vector pointing from the origin in polar coordinates
- θunit = unit vector pointing in the direction of increasing values of theta in polar coordinates
Note: All quantities in bold represent vectors.]
Center of mass
Discrete case:
where n is the number of mass particles.
Continuous case:
where ρ(s) is the scalar mass density as a function of the position vector
Velocity
Acceleration
- Centripetal Acceleration
(R = radius of the circle, ω = v/R angular velocity)
Momentum
Force
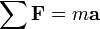 (Constant Mass)
(Constant Mass)
Impulse
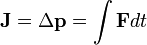
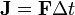 if F is constant
if F is constant
Moment of inertia
For a single axis of rotation: The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
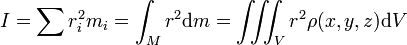
Angular momentum
- if v is perpendicular to r
Vector form:
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor of rank-2)
r is the radius vector.
Torque
if |r| and the sine of the angle between r and p remains constant.
This one is very limited, more added later. α = dω/dt
Precession
Omega is called the precession angular speed, and is defined:
(Note: w is the weight of the spinning flywheel)
Energy
for m as a constant:
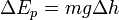 in field of gravity
in field of gravity
Central force motion
Equations of motion (constant acceleration)
These equations can be used only when acceleration is constant. If acceleration is not constant then calculus must be used.
These equations can be adapted for angular motion, where angular acceleration is constant:
LIMITS OF VALIDITY
Limits of validity
Many branches of classical mechanics are simplifications or approximations of more accurate forms; two of the most accurate being general relativity and relativistic statistical mechanics. Geometric optics is an approximation to the quantum theory of light, and does not have a superior "classical" form.
The Newtonian approximation to special relativity
In special relativity, the momentum of a particle is given by
where m is the particle's mass, v its velocity, and c is the speed of light.
If v is very small compared to c, v2/c2 is approximately zero, and so
Thus the Newtonian equation p = mv is an approximation of the relativistic equation for bodies moving with low speeds compared to the speed of light.
For example, the relativistic cyclotron frequency of a cyclotron, gyrotron, or high voltage magnetron is given by
where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest) mass m0 circling in a magnetic field. The (rest) mass of an electron is 511 keV. So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV direct current accelerating voltage.
The classical approximation to quantum mechanics
The ray approximation of classical mechanics breaks down when the de Broglie wavelength is not much smaller than other dimensions of the system. For non-relativistic particles, this wavelength is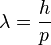
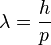
where h is Planck's constant and p is the momentum.
Again, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson and Lester Germer in 1927, accelerated by 54 volts, had a wave length of 0.167 nm, which was long enough to exhibit a single diffraction side lobe when reflecting from the face of a nickel crystal with atomic spacing of 0.215 nm. With a larger vacuum chamber, it would seem relatively easy to increase the angular resolution from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuitcomputer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diodes and very narrow transistor gates in integrated circuits.
Classical mechanics is the same extreme high frequency approximation as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
WORK AND ENERGY
If a constant force F is applied to a particle that achieves a displacement Δr, the work done by the force is defined as the scalar product of the force and displacement vectors:
More generally, if the force varies as a function of position as the particle moves from r1 to r2 along a path C, the work done on the particle is given by the line integral
If the work done in moving the particle from r1 to r2 is the same no matter what path is taken, the force is said to be conservative. Gravity is a conservative force, as is the force due to an idealized spring, as given by Hooke's law. The force due to friction is non-conservative.
The kinetic energy Ek of a particle of mass m travelling at speed v is given by
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
The work-energy theorem states that for a particle of constant mass m the total work W done on the particle from position r1 to r2 is equal to the change in kinetic energy Ek of the particle:
Conservative forces can be expressed as the gradient of a scalar function, known as the potential energy and denoted Ep:
If all the forces acting on a particle are conservative, and Ep is the total potential energy (which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
This result is known as conservation of energy and states that the total energy,
is constant in time. It is often useful, because many commonly encountered forces are conservative.
FORCES-NEWTONS SECOND LAW
Newton was the first to mathematically express the relationship between force and momentum. Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it to be a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":
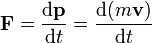 .
.
The quantity mv is called the (canonical) momentum. The net force on a particle is thus equal to rate change of momentum of the particle with time. Since the definition of acceleration is a = dv/dt, the second law can be written in the simplified and more familiar form:
So long as the force acting on a particle is known, Newton's second law is sufficient to describe the motion of a particle. Once independent relations for each force acting on a particle are available, they can be substituted into Newton's second law to obtain an ordinary differential equation, which is called the equation of motion.
As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
where λ is a positive constant. Then the equation of motion is
This can be integrated to obtain
where v0 is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy), slowing it down. This expression can be further integrated to obtain the position r of the particle as a function of time.
Important forces include the gravitational force and the Lorentz force for electromagnetism. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force F on another particle B, it follows that B must exert an equal and opposite reaction force, −F, on A. The strong form of Newton's third law requires that F and −F act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
CLASSICAL MECHANICS-VELOCITY, FORCE, ACCELERATION, FRAMES OF REFERENCE
Description of the theory

The analysis of projectile motion is a part of classical mechanics.
The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects which classical mechanics can describe always have a non-zerosize. (The physics of very small particles, such as the electron, is more accurately described byquantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseballcan spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.
Velocity and speed
The position of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle. In general, the point particle need not be stationary relative to O, so r is a function of t, the timeelapsed since an arbitrary initial time. In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumesEuclidean geometry for the structure of space.
The velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time or
In classical mechanics, velocities are directly additive and subtractive. For example, if one car traveling East at 60 km/h passes another car traveling East at 50 km/h, then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, from the perspective of the faster car, the slower car is moving 10 km/h to the West. Velocities are directly additive as vector quantities; they must be dealt with using vector analysis.
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector u = ud and the velocity of the second object by the vector v = ve, where u is the speed of the first object, v is the speed of the second object, and d and e are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is
Similarly,
When both objects are moving in the same direction, this equation can be simplified to
Or, by ignoring direction, the difference can be given in terms of speed only:
Acceleration
The acceleration, or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time) or
Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both. If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration, but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.
Frames of reference
While the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames. They are characterized by the absence of acceleration of the observer and the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth). A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame. A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are unaccelerated with respect to the distant stars are regarded as good approximations to inertial frames.
Consider two reference frames S and S' . For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x′,y′,z′,t′) in frame S′. Assuming time is measured the same in all reference frames, and if we require x = x' when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S′ and S, which are moving at a relative velocity of u in the x direction is:
- x′ = x − ut
- y′ = y
- z′ = z
- t′ = t
This set of formulas defines a group transformation known as the Galilean transformation (informally, the Galilean transform). This group is a limiting case of the Poincaré group used in special relativity. The limiting case applies when the velocity u is very small compared to c, thespeed of light.
The transformations have the following consequences:
- v′ = v − u (the velocity v′ of a particle from the perspective of S′ is slower by u than its velocity v from the perspective of S)
- a′ = a (the acceleration of a particle is the same in any inertial reference frame)
- F′ = F (the force on a particle is the same in any inertial reference frame)
- the speed of light is not a constant in classical mechanics, nor does the special position given to the speed of light in relativistic mechanics have a counterpart in classical mechanics.
Subscribe to:
Comments (Atom)

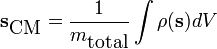

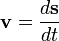
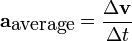
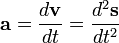
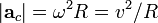

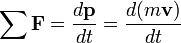

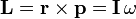

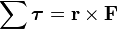

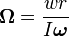
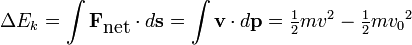
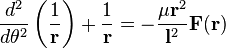
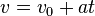
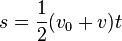

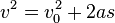
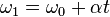
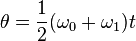
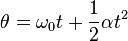

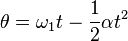


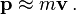



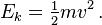


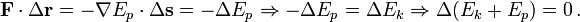

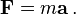



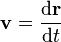 .
.



 .
.