Wednesday, August 18, 2010

FLUID FLOW AND AIR SPEED MEASUREMENTS(BERNOULLI'S THEORY)

Daniel Bernoulli, a Swiss mathematician, stated a principle that describes the relationship between internal fluid pressure and fluid velocity. His principle, essentially a statement of the conversation of energy, explains at least in part why an airfoil develops an aerodynamic force.
All of the forces acting on a surface over which there is a flow of air are the result of skin friction or pressure. Friction forces are the result of viscosity and are confined to a very thin layer of air near the surface. They usually are not dominant and, from the aviator's perspective, can be discounted.
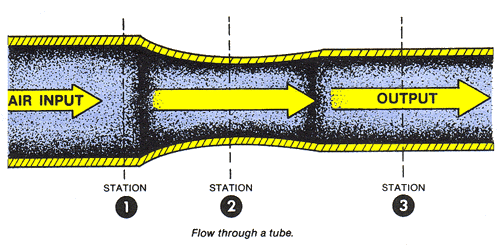
As an aid in visualizing what happens to pressure as air flows over an airfoil, it is helpful to consider flow through a tube (Please see Figure above). The concept of conservation of mass states that mass cannot be created or destroyed; so, what goes in one end of the tube must come out the other end. If the flow through a tube is neither acccelerating or decelerating at the input, then the mass of flow per unit of time at Station 1 must equal the mass of flow per unit of time at Station 2, and so on, through Station 3. The mass of flow per unit area (cross-sectional area of tube) is called the Mass Flow Rate.
At low flight speeds, air experiences relatively small changes in pressure and negligable changes in density. This airflow is termed incompressable since the air may undergo changes in pressure without apparent changes in density. Such airflow is similar to the flow of water, hydraulic fluid, or any other incompressable fluid. This suggests that between any two points in the tube, the velocity varies inversely with the area. Venturi effectis the name used to describe this phenomenon. Fluid flow speeds up through the restricted area of a venturi in direct proportion to the reduction in area. The Figure below suggests what happens to the speed of the flow through the tube discussed.


The total energy in a given closed system does not change, but the form of the energy may be altered. The pressure of the flowing air may be likened to energy in that the total pressure of flowing air will always remain constant unless energy is added or taken from the flow. In the previous examples there is no addition or subtraction of energy; therefore the total pressure will remain constant.
Fluid flow pressure is made up of two componants - Static pressure and dynamic pressure. The Static Pressure is that measured by an aneroid barometer placed in the flow but not moving with the flow. The Dynamic Pressure of the flow is that componant of total pressure due to motion of the air. It is difficult to measure directly, but a pitot-static tub emeasures it indirectly. The sume of these two pressures is total pressure and is measured by allowing the flow to impact against an open-end tube which is venter to an aneroid barometer. This is the incompressible or slow-speed form of the Bernoulli equation.
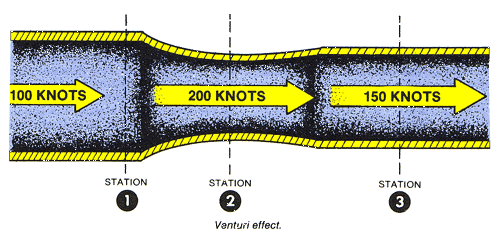
Static pressure decreases as the velocity increases. This is what happens to air passing over the curved top of an aircraft's airfoil. Consider only the bottom half of a venturi tube in the Figure below. Notice how the shape of the restricted area at Station 2 resembles the top surface of an airfoil. Even when the top half of the venturi tube is taken away, the air still accelerates over the curved shape of the bottom half. This happens because the air layers restrict the flow just as did the top half of the venturi tube. As a result, acceleration causes decreased static pressure above the curved shape of the tube. A pressure differential force is generated by the local variation of static and dynamic pressures on the curved surface.

A comparison can be made with water flowing thru a garden hose. Water moving through a hose of constant diameter exerts a uniform pressure on the hose; but if the diameter of a section of the hose in increased or decreased, it is certain to change the pressure of the water at this point. Suppose we were to pinch the hose, therby constricting the area through which the water flows. Assuming that the same volume of water flows through the constricted portion of the hose in the same period of time as before the hose was pinched, it follows that the speed of flow must increase at that point. If we constrict a portion of the hose, we not only increase the speed of the flow, but we also decrease the pressure at that point. We could achieve like results if we were to introduce streamlined solids (airfoils) at the same point in the hose. This principle is the basis for measuring airspeed (fluid flow) and for analyzing the airfoil's ability to produce lift.
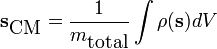
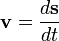
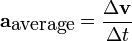
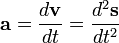
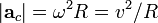
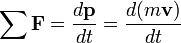
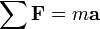
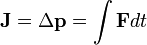
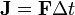
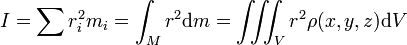
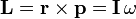
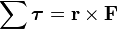
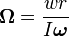
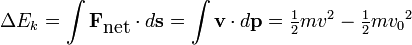
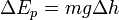
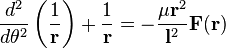
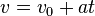
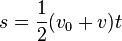
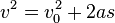
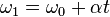
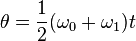
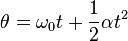
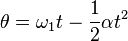
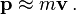
Posted by at No comments:

Saturday, June 26, 2010

Posted by at No comments:

Friday, June 25, 2010

List of equations in classical mechanics


Nomenclature
a = acceleration (m/s²)
g = gravitational field strength/acceleration in free-fall (m/s²)
F = force (N = kg m/s²)
Ek = kinetic energy (J = kg m²/s²)
Ep = potential energy (J = kg m²/s²)
m = mass (kg)
p = momentum (kg m/s)
s = displacement (m)
R = radius (m)
t = time (s)
v = velocity (m/s)
v0 = velocity at time t=0
W = work (J = kg m²/s²)
τ = torque (m N, not J) (torque is the rotational form of force)
s(t) = position at time t
s0 = position at time t=0
runit = unit vector pointing from the origin in polar coordinates
θunit = unit vector pointing in the direction of increasing values of theta in polar coordinates
Note: All quantities in bold represent vectors.]
Center of mass
Discrete case:



\mathbf{s}_{\hbox{CM}} = {1 \over m_{\hbox{total}}} \sum_{i = 1}^{n} m_i \mathbf{s}_i
where n is the number of mass particles.
Continuous case:
\mathbf{s}_{\hbox{CM}} = {1 \over m_{\hbox{total}}} \int \rho(\mathbf{s}) dV
where ρ(s) is the scalar mass density as a function of the position vector

Velocity

\mathbf{v}_{\mbox{average}} = {\Delta \mathbf{d} \over \Delta t}
\mathbf{v} = {d\mathbf{s} \over dt}


Acceleration

\mathbf{a}_{\mbox{average}} = \frac{\Delta\mathbf{v}}{\Delta t}
\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d^2\mathbf{s}}{dt^2}
  • Centripetal Acceleration
|\mathbf{a}_c | = \omega^2 R = v^2 / R
(R = radius of the circle, ω = v/R angular velocity)

Momentum

\mathbf{p} = m\mathbf{v}


Force

\sum \mathbf{F} = \frac{d\mathbf{p}}{dt} = \frac{d(m\mathbf{v})}{dt}
\sum \mathbf{F} = m\mathbf{a} \quad\    (Constant Mass)


Impulse

\mathbf{J} = \Delta \mathbf{p} = \int \mathbf{F} dt
\mathbf{J} = \mathbf{F} \Delta t \quad\
   if F is constant


Moment of inertia

For a single axis of rotation: The moment of inertia for an object is the sum of the products of the mass element and the square of their distances from the axis of rotation:
I = \sum r_i^2 m_i =\int_M r^2 \mathrm{d} m = \iiint_V r^2 \rho(x,y,z) \mathrm{d} V


Angular momentum

|L| = mvr \quad\
   if v is perpendicular to r
Vector form:
\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{I}\, \omega
(Note: I can be treated like a vector if it is diagonalized first, but it is actually a 3×3 matrix - a tensor of rank-2)
r is the radius vector.


Torque

\sum \boldsymbol{\tau} = \frac{d\mathbf{L}}{dt}
\sum \boldsymbol{\tau} = \mathbf{r} \times \mathbf{F} \quad
if |r| and the sine of the angle between r and p remains constant.
\sum \boldsymbol{\tau} = \mathbf{I} \boldsymbol{\alpha}
This one is very limited, more added later. α = dω/dt


Precession

Omega is called the precession angular speed, and is defined:
\boldsymbol{\Omega} = \frac{wr}{I\boldsymbol{\omega}}
(Note: w is the weight of the spinning flywheel)

Energy

for m as a constant:
\Delta E_k = \int \mathbf{F}_{\mbox{net}} \cdot d\mathbf{s} = \int \mathbf{v} \cdot d\mathbf{p} = \begin{matrix}\frac{1}{2}\end{matrix} mv^2 - \begin{matrix}\frac{1}{2}\end{matrix} m{v_0}^2 \quad\
\Delta E_p = mg\Delta h \quad\ \,\! in field of gravity


Central force motion

\frac{d^2}{d\theta^2}\left(\frac{1}{\mathbf{r}}\right) + \frac{1}{\mathbf{r}} = -\frac{\mu\mathbf{r}^2}{\mathbf{l}^2}\mathbf{F}(\mathbf{r})


Equations of motion (constant acceleration)

These equations can be used only when acceleration is constant. If acceleration is not constant then calculus must be used.
v = v_0+at \,
s = \frac {1} {2}(v_0+v) t
s = v_0 t + \frac {1} {2} a t^2
v^2 = v_0^2 + 2 a s \,
These equations can be adapted for angular motion, where angular acceleration is constant:
\omega _1 = \omega _0 + \alpha t \,
\theta = \frac{1}{2}(\omega _0 + \omega _1)t
\theta = \omega _0 t + \frac{1}{2} \alpha t^2
\omega _1^2 = \omega _0^2 + 2\alpha\theta
\theta = \omega _1 t - \frac{1}{2} \alpha t^2
Posted by at No comments:

LIMITS OF VALIDITY


Limits of validity


Domain of validity for Classical Mechanics
Many branches of classical mechanics are simplifications or approximations of more accurate forms; two of the most accurate being general relativity and relativistic statistical mechanics. Geometric optics is an approximation to the quantum theory of light, and does not have a superior "classical" form.


The Newtonian approximation to special relativity

In special relativity, the momentum of a particle is given by
\mathbf{p} = \frac{m \mathbf{v}}{ \sqrt{1-v^2/c^2}} \, ,
where m is the particle's mass, v its velocity, and c is the speed of light.
If v is very small compared to c, v2/c2 is approximately zero, and so
\mathbf{p} \approx m\mathbf{v} \, .
Thus the Newtonian equation p = mv is an approximation of the relativistic equation for bodies moving with low speeds compared to the speed of light.
For example, the relativistic cyclotron frequency of a cyclotron, gyrotron, or high voltage magnetron is given by
f=f_c\frac{m_0}{m_0+T/c^2} \, ,
where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest) mass m0 circling in a magnetic field. The (rest) mass of an electron is 511 keV. So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV direct current accelerating voltage.

The classical approximation to quantum mechanics

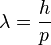
The ray approximation of classical mechanics breaks down when the de Broglie wavelength is not much smaller than other dimensions of the system. For non-relativistic particles, this wavelength is\lambda=\frac{h}{p}
where h is Planck's constant and p is the momentum.
Again, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson and Lester Germer in 1927, accelerated by 54 volts, had a wave length of 0.167 nm, which was long enough to exhibit a single diffraction side lobe when reflecting from the face of a nickel crystal with atomic spacing of 0.215 nm. With a larger vacuum chamber, it would seem relatively easy to increase the angular resolution from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuitcomputer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diodes and very narrow transistor gates in integrated circuits.
Classical mechanics is the same extreme high frequency approximation as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
Posted by at No comments:

WORK AND ENERGY


If a constant force F is applied to a particle that achieves a displacement Δr, the work done by the force is defined as the scalar product of the force and displacement vectors:
W = \mathbf{F} \cdot \Delta \mathbf{r} \, .
More generally, if the force varies as a function of position as the particle moves from r1 to r2 along a path C, the work done on the particle is given by the line integral
W = \int_C \mathbf{F}(\mathbf{r}) \cdot \mathrm{d}\mathbf{r} \, .
If the work done in moving the particle from r1 to r2 is the same no matter what path is taken, the force is said to be conservative. Gravity is a conservative force, as is the force due to an idealized spring, as given by Hooke's law. The force due to friction is non-conservative.
The kinetic energy Ek of a particle of mass m travelling at speed v is given by
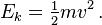
E_k = \tfrac{1}{2}mv^2 \, .
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
The work-energy theorem states that for a particle of constant mass m the total work W done on the particle from position r1 to r2 is equal to the change in kinetic energy Ek of the particle:
W = \Delta E_k = E_{k,2} - E_{k,1} = \tfrac{1}{2}m\left(v_2^{\, 2} - v_1^{\, 2}\right) \, .
Conservative forces can be expressed as the gradient of a scalar function, known as the potential energy and denoted Ep:
\mathbf{F} = - \mathbf{\nabla} E_p \, .
If all the forces acting on a particle are conservative, and Ep is the total potential energy (which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
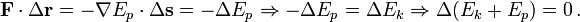
\mathbf{F} \cdot \Delta \mathbf{r} = - \mathbf{\nabla} E_p \cdot \Delta \mathbf{s} = - \Delta E_p \Rightarrow - \Delta E_p = \Delta E_k \Rightarrow \Delta (E_k + E_p) = 0 \, .
This result is known as conservation of energy and states that the total energy,
\sum E = E_k + E_p \, .
is constant in time. It is often useful, because many commonly encountered forces are conservative.
Posted by at No comments:

FORCES-NEWTONS SECOND LAW


Newton was the first to mathematically express the relationship between force and momentum. Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it to be a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":
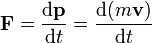\mathbf{F} = {\mathrm{d}\mathbf{p} \over \mathrm{d}t} = {\mathrm{d}(m \mathbf{v}) \over \mathrm{d}t}.
The quantity mv is called the (canonical) momentum. The net force on a particle is thus equal to rate change of momentum of the particle with time. Since the definition of acceleration is a = dv/dt, the second law can be written in the simplified and more familiar form:
\mathbf{F} = m \mathbf{a} \, .
So long as the force acting on a particle is known, Newton's second law is sufficient to describe the motion of a particle. Once independent relations for each force acting on a particle are available, they can be substituted into Newton's second law to obtain an ordinary differential equation, which is called the equation of motion.
As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
\mathbf{F}_{\rm R} = - \lambda \mathbf{v} \, ,
where λ is a positive constant. Then the equation of motion is
- \lambda \mathbf{v} = m \mathbf{a} = m {\mathrm{d}\mathbf{v} \over \mathrm{d}t} \, .
This can be integrated to obtain
\mathbf{v} = \mathbf{v}_0 e^{- \lambda t / m}
where v0 is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy), slowing it down. This expression can be further integrated to obtain the position r of the particle as a function of time.
Important forces include the gravitational force and the Lorentz force for electromagnetism. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force F on another particle B, it follows that B must exert an equal and opposite reaction force, −F, on A. The strong form of Newton's third law requires that F and −F act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
Posted by at No comments:
Subscribe to: Posts (Atom)