Daniel Bernoulli, a Swiss mathematician, stated a principle that describes the relationship between internal fluid pressure and fluid velocity. His principle, essentially a statement of the conversation of energy, explains at least in part why an airfoil develops an aerodynamic force.
All of the forces acting on a surface over which there is a flow of air are the result of skin friction or pressure. Friction forces are the result of viscosity and are confined to a very thin layer of air near the surface. They usually are not dominant and, from the aviator's perspective, can be discounted.
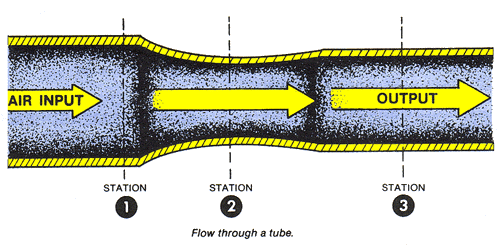
At low flight speeds, air experiences relatively small changes in pressure and negligable changes in density. This airflow is termed incompressable since the air may undergo changes in pressure without apparent changes in density. Such airflow is similar to the flow of water, hydraulic fluid, or any other incompressable fluid. This suggests that between any two points in the tube, the velocity varies inversely with the area. Venturi effectis the name used to describe this phenomenon. Fluid flow speeds up through the restricted area of a venturi in direct proportion to the reduction in area. The Figure below suggests what happens to the speed of the flow through the tube discussed.
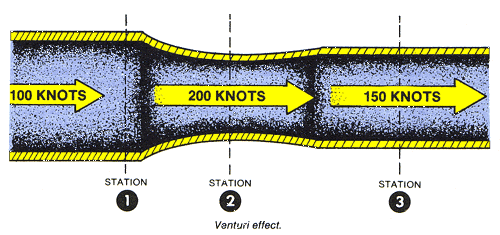
The total energy in a given closed system does not change, but the form of the energy may be altered. The pressure of the flowing air may be likened to energy in that the total pressure of flowing air will always remain constant unless energy is added or taken from the flow. In the previous examples there is no addition or subtraction of energy; therefore the total pressure will remain constant.
Fluid flow pressure is made up of two componants - Static pressure and dynamic pressure. The Static Pressure is that measured by an aneroid barometer placed in the flow but not moving with the flow. The Dynamic Pressure of the flow is that componant of total pressure due to motion of the air. It is difficult to measure directly, but a pitot-static tub emeasures it indirectly. The sume of these two pressures is total pressure and is measured by allowing the flow to impact against an open-end tube which is venter to an aneroid barometer. This is the incompressible or slow-speed form of the Bernoulli equation.
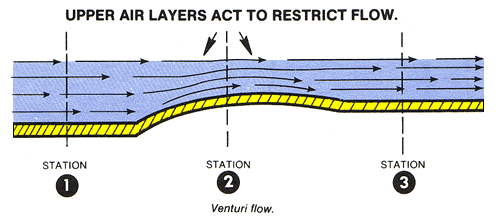
Static pressure decreases as the velocity increases. This is what happens to air passing over the curved top of an aircraft's airfoil. Consider only the bottom half of a venturi tube in the Figure below. Notice how the shape of the restricted area at Station 2 resembles the top surface of an airfoil. Even when the top half of the venturi tube is taken away, the air still accelerates over the curved shape of the bottom half. This happens because the air layers restrict the flow just as did the top half of the venturi tube. As a result, acceleration causes decreased static pressure above the curved shape of the tube. A pressure differential force is generated by the local variation of static and dynamic pressures on the curved surface.
A comparison can be made with water flowing thru a garden hose. Water moving through a hose of constant diameter exerts a uniform pressure on the hose; but if the diameter of a section of the hose in increased or decreased, it is certain to change the pressure of the water at this point. Suppose we were to pinch the hose, therby constricting the area through which the water flows. Assuming that the same volume of water flows through the constricted portion of the hose in the same period of time as before the hose was pinched, it follows that the speed of flow must increase at that point. If we constrict a portion of the hose, we not only increase the speed of the flow, but we also decrease the pressure at that point. We could achieve like results if we were to introduce streamlined solids (airfoils) at the same point in the hose. This principle is the basis for measuring airspeed (fluid flow) and for analyzing the airfoil's ability to produce lift.